Поверхности вращения
К поверхностям вращения относятся поверхности, образующиеся вращением линии l вокруг прямой i, представляющей собой ось вращения. Они могут быть линейчатыми, например конус или цилиндр вращения, и нелинейчатыми или криволинейными, например сфера. Определитель поверхности вращения включает образующую l и ось i. Криволинейная поверхность вращения образуется при вращении лю-
Каждая точка образующей при вращении описывает окружность, плоскость которой перпендикулярна оси вращения. Такие окружности поверхности вращения называются параллелями. Наибольшую из параллелей называют экватором. Экватор .определяет горизонтальный очерк поверхности, если i _|_ П1. В этом случае параллелями являются горизонтали h этой поверхности.
Кривые поверхности вращения, образующиеся в результате пересечения поверхности плоскостями, проходящими через ось вращения, называются меридианами. Все меридианы одной поверхности конгруэнтны. Фронтальный меридиан называют главным меридианом; он определяет фронтальный очерк поверхности вращения. Профильный меридиан определяет профильный очерк поверхности вращения.
Строить точку на криволинейных поверхностях вращения удобнее всего с помощью параллелей поверхности. На рис. 103 точка М построена на параллели h4.
Поверхности вращения нашли самое широкое применение в технике. Они ограничивают поверхности большинства машиностроительных деталей.
Коническая поверхность вращения образуется вращением прямой i вокруг пересекающейся с ней прямой — оси i (рис. 104, а). Точка М на поверхности построена с помощью образующей l и параллели h. Эту поверхность называют еще конусом вращения или прямым круговым конусом.
Цилиндрическая поверхность вращения образуется вращением прямой l вокруг параллельной ей оси i (рис. 104, б). Эту поверхность называют еще цилиндром или прямым круговым цилиндром.
Сфера, образуется вращением окружности вокруг ее диаметра (рис. 104, в). Точка A на поверхности сферы принадлежит главному
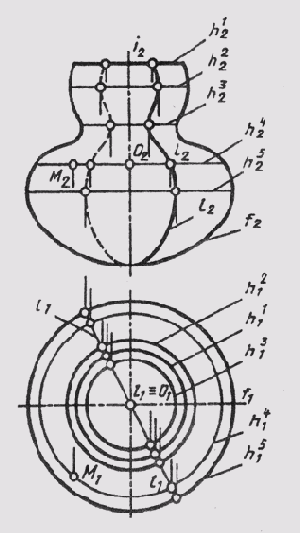
Рис. 103
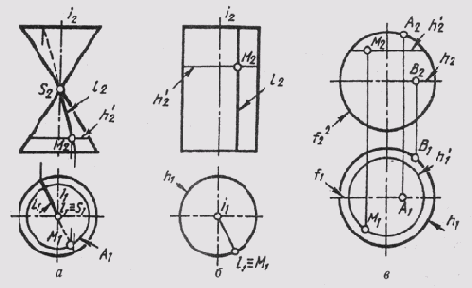
Рис. 104
меридиану f, точка В — экватору h, а точка М построена на вспомогательной параллели h'.
Тор образуется вращением окружности или ее дуги вокруг оси, лежащей в плоскости окружности. Если ось расположена в пределах образующейся окружности, то такой тор называется закрытым (рис. 105, а). Если ось вращения находится вне окружности, то такой тор называется открытым (рис. 105, б). Открытый тор называется еще кольцом.
Поверхности вращения могут быть образованы и другими кривыми второго порядка. Эллипсоид вращения (рис. 106, а) образуется вращением эллипса вокруг одной из его осей; параболоид вращения (рис. 106, б) — вращением параболы вокруг ее оси; гиперболоид вращения однополостный (рис. 106, в) образуется вращением гиперболы вокруг мнимой оси, а двуполостный (рис. 106, г) — вращением гиперболы вокруг действительной оси.
В общем случае поверхности изображаются не ограниченными в направлении распространения образующих линий (см. рис. 97, 98). Для решения конкретных задач и получения геометрических фигур ограничиваются плоскостями обреза. Например, чтобы получить круговой цилиндр, необходимо ограничить участок цилиндрической поверхности плоскостями обреза (см. рис. 104, б). В результате получим его верхнее и нижнее основания. Если плоскости обреза перпендикулярны оси вращения, цилиндр будет прямым, если нет — цилиндр будет наклонным.
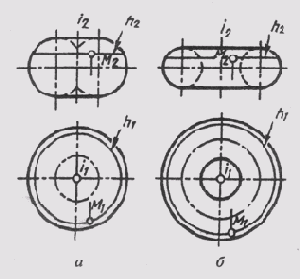
Рис. 105
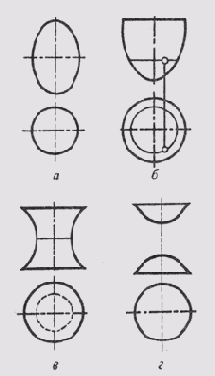
Рис. 106
Чтобы получить круговой конус (см. рис. 104, а), необходимо выполнить обрез по вершине и за пределами ее. Если плоскость обреза основания цилиндра будет перпендикулярна оси вращения — конус будет прямой, если нет — наклонный. Если обе плоскости обреза не проходят через вершину — конус получим усеченным.
С помощью плоскости обреза можно получить призму и пирамиду. Например, шестигранная пирамида будет прямой, если все ее ребра имеют одинаковый наклон к плоскости обреза. В других случаях она будет наклонной. Если она выполнена с помощью плоскостей обреза и ни одна из них не проходит через вершину — пирамида усеченная.
Призму (см. рис. 101) можно получить, ограничив участок призматической поверхности двумя плоскостями обреза.Если плоскость обреза перпендикулярна ребрам, например восьмигранной призмы, она прямая, если не перпендикулярна — наклонная.
Выбирая соответствующее положение плоскостей обреза, можно получать различные формы геометрических фигур в зависимости от условий решаемой задачи.